大纲：

• 交换两个变量
• 输出10个数中的最大数
• 有3个数a, b, c， 要求按有大小顺序把他们输出
• 求1+2+3+……+100
• 判断一个数n能否同时被3和5整除
• 求两个数m和n的最大公约数
• 求一元二次方程式ax^2+bx+c=0的根，分别考虑有两个不相等的实根和有两个相等的实根两种情况

前言

温馨提示：部分运算符号和书上会有出入，可能是因为学的算法版本不一致的原因…

注意：仅供参考，和标准答案多少会有点出入，而且算法的答案本身就不唯一！！！

注意：仅供参考，和标准答案多少会有点出入，而且算法的答案本身就不唯一！！！

注意：仅供参考，和标准答案多少会有点出入，而且算法的答案本身就不唯一！！！

由于只是我一个人的力量，当时我学c语言的时候，算法这一章就是一带而过的emmmmm，纯属是自己看的课本，现学的，还要就是第一次学画NS图，八张图下来，已经熟练啦，你会发现后面画的图还是可以看的过去的哈哈哈哈

如果出现错误纯属正常哈~ 如果有什么不明白的地方，可以联系我，关于页面有我的联系方式哈或者可以在评论区留言也行哦（回复较慢）！

电脑画图软件

• 流程图：draw.io
• NS流程图：亿图图示

第一题

有两个瓶子a和b，分别盛放醋和酱油，要求将它们互换。

问题分析

注意：此处的瓶子是两个装满东西的瓶子，不能混掺，所以要想交换就得再拿一个空瓶子用来临时存放。现假设：A中装满了醋，B中装满了酱油，C是临时存放的空瓶子。

• 第一步：把A中的醋倒入空瓶子C中，临时保存。（A瓶此时已经空了，接下来就可以把B中的酱油倒进来了）
• 第二步：把B中的酱油倒入A瓶中（B瓶此时也空了，接下来可以把C中暂存的醋倒进来啦）
• 第三步：把C中的醋倒入B中（到此，就已经实现了醋和酱油的交换。）

这是一道很经典的算法题，一旦涉及到两数交换，基本就是这个算法了。

流程图

NS图

第二题

依次将10个数输入，要求输出其中最大的数。

问题分析

我们可以声明一个max变量用来存放10个数当中最大的数，如果输入的数比max大就赋值给max，否则就不赋值。那么问题来了，既然需要跟max比较，那就要在比较之前先给定max一个具体的值吧，要不然怎么和max比较呢？你说是吧。 那究竟给什么值合适呢？

可以随意给max赋值吗？答案是否定的！！！ 为什么呢？

你想，加入我们给max赋值为0，而我们输入的十个数 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10,都比max小，不会把max替换掉，导致我们最终得到的结果就是max为0，也就是十个数中的最大数是0，显然，这是错误的。

这里，我们可以假设第一次输入的数最大，我说的是假设哦~ 如果它不是最大的话就被后面比它大的数替换了呗，对吧。我们一样可以找出最大。 相信到这里你已经明白了我的思路

• 把第一次输入的值赋值给max
• i 从 1 开始，一共需要输入10个数，我们已经把第一个输入的数给了max 所以还剩下9个数也就是说循环还剩下就此，即i应该≤9！！！而不是≤10！！！ 这是第二个易错点！！！
• 每循环一次，都需要比较一下输入的数是否大于max，如果大于，就用新输入的数把max换掉，更新最大值。
• 循环结束，max肯定就是10个数中的最大值了，这个时候就可以把最大值输入出来了。

流程图

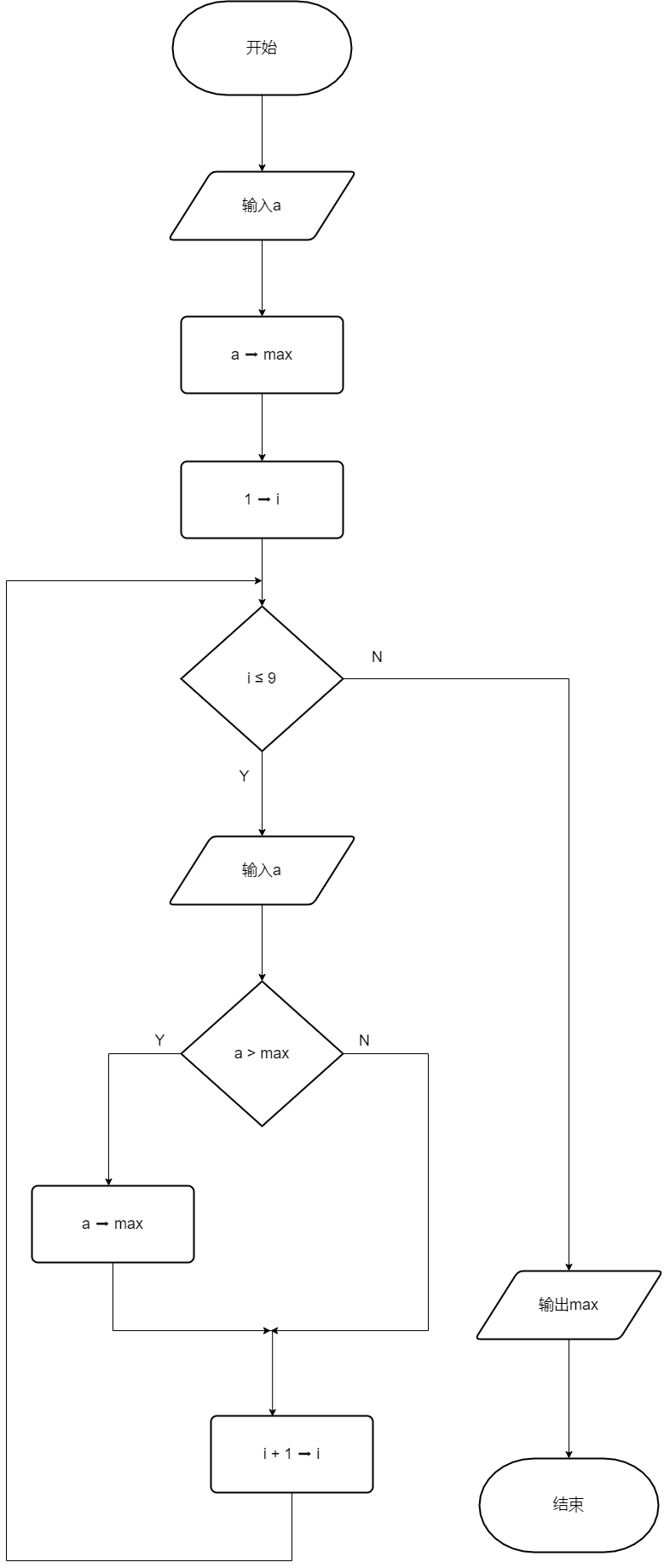
NS图

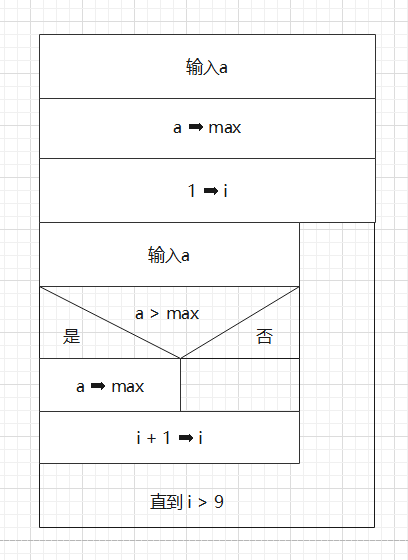
很抱歉：刚发现一个小错误，这个NS图的最后，少了一个输出max，自行补上哈！电脑画NS图实在太费劲了…，见谅哈！

第三题

有3个数a, b, c， 要求按有大小顺序把他们输出。

问题分析

这道题流程图采用的算法和NS图采用的算法不一样哦！具体看我下面分析哈。

流程图的算法：想要按大小顺序输出a，b，c三个数，这里我们按照由大到小来输出，由小到大只需要改一下输出顺序即可哈。

• 第一步确定a和b的大小关系，保证a一定大于b，如果a不大于b，就让a和b的数交换，用到问题一的算法即可。换完之后不就保证a最大了嘛，是吧。
• 为什么一定要保证a大于b呢，如果不这样的话，结果就太复杂了，3个数全排列，6中结果，但我们让a一定大于b的话，结果就只有三种啦，也是一个技巧吧！
• 接下来我们再分别判断a和c的关系，b和c的关系就行啦，至于a和b，咱们已经保证了a一定大于b啦。就不用在判断啦~

NS图的算法：同上，这儿的输出结果也是由大到小哦。这里采用的算法是把a，b，c的大小关系都锁死，流程图的那种算法会出现三种结果，而如果我们把a,b,c的大小关系限制死，即a最大，b中间，c最小的话就只有一种结果啦。

• 首先保证a和b的大小关系，如果a小于b，就让二者交换。
• 接下来保证a和c的大小关系，如果a小于c，就让二者交换。到这里a就可以做到最大了。
• 接下来的任务就是让b处于中间，它已经比a小了，怎么让它处于中间呢？
• 很简单，保证b比c大即可。方法同上，如果b小于c就让二者交换。
• 注意：二者交换的算法就是问题一的算法哈。忘了的话再回到上面看一下。

流程图

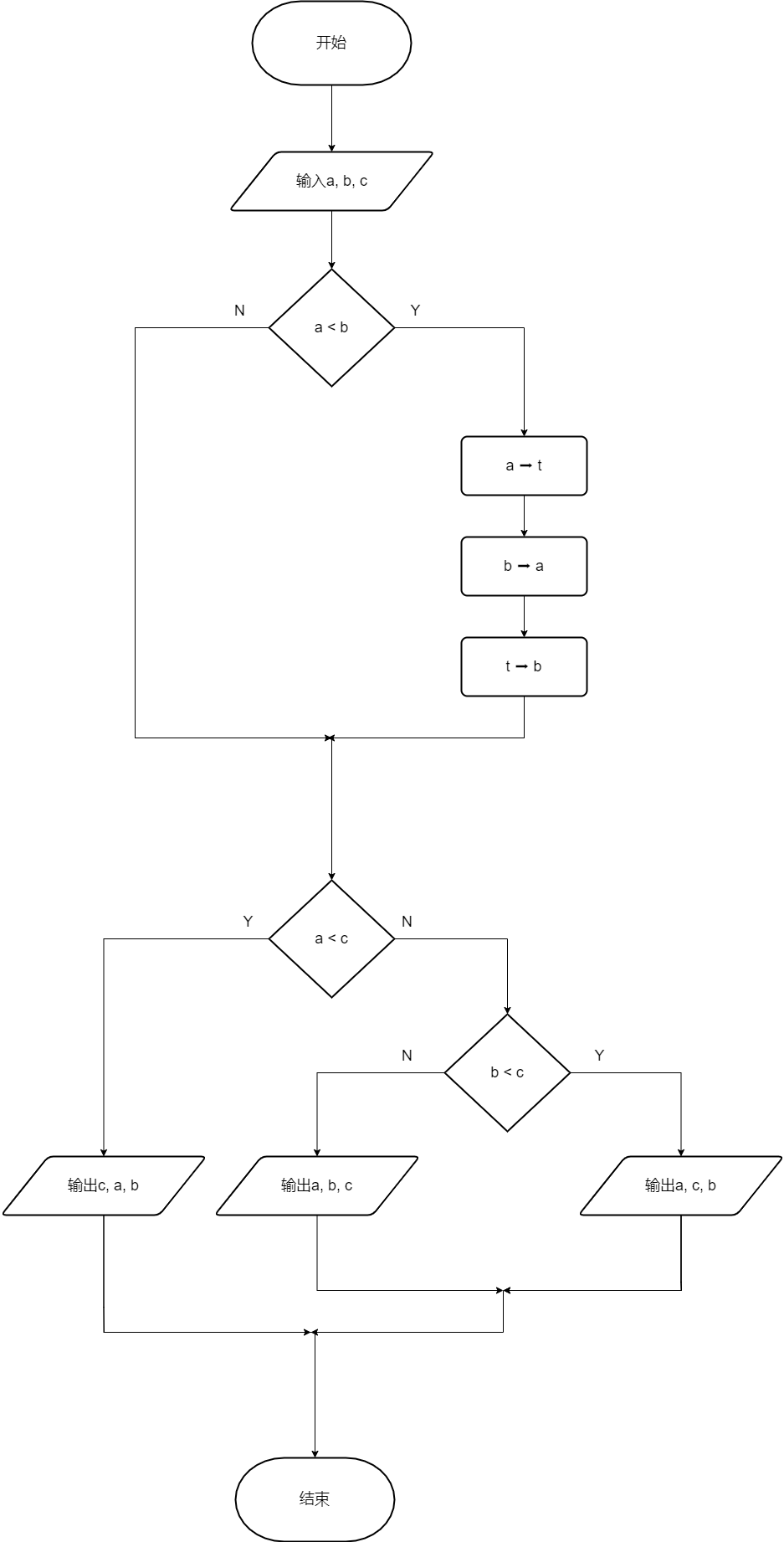
NS图

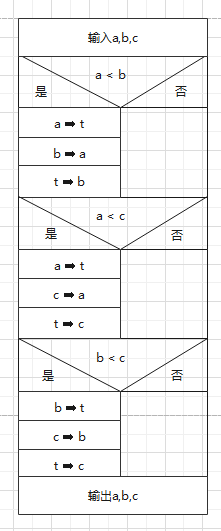
第四题

求1+2+3+……+100。

问题分析

这道题很简单，就是求1-100求和，我们需要用一个变量S（sum的缩写）来存放1-100的和。

计算机就是用来算这种繁琐的题目的，总不能人工一个一个数的加吧，再快点无非就是用数学公式，但老师想考我们的是循环哦~

注意：在加法求和中S尝尝初始值为0，乘法常常初始值为1。这个很好理解吧。求和+0没影响，求积x1没影响，是吧。

方法步骤：

• 初始化S为0，i 为1 //因为从1开始加
• 循环100次，i 从1 ≤ 100
• 每次循环先让每次的 i 值加到S里，然后再让 i 自身+1
• 注意：NS图里的i > 100是终止条件哦！ 别弄混啦~

流程图

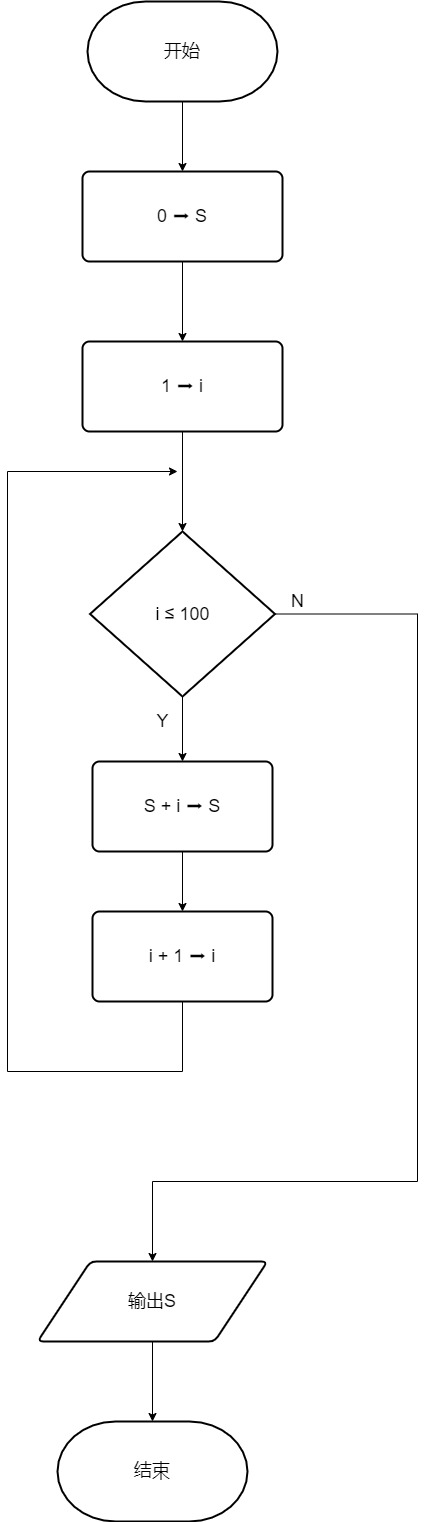
NS图

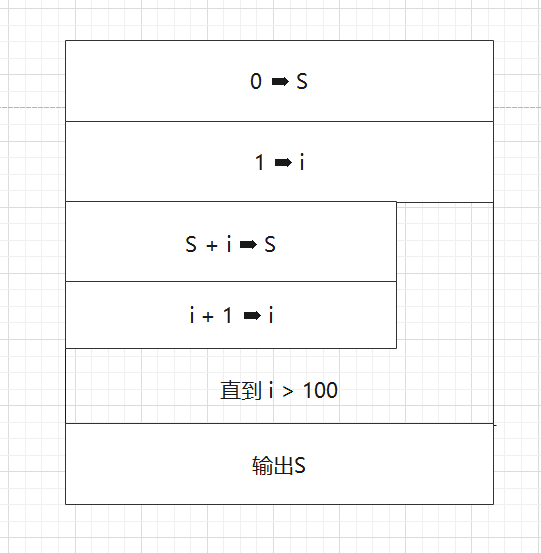
第五题

判断一个数n能否同时被3和5整除。

问题分析

个人觉得这个算法太简单了，没什么好分析的，老师出这道题的目的就是想让大家多练习一下流程图和NS图的规则吧~ emmmmm 毕竟是初学者，认真画好好画就行了，我觉得大家应该都能看懂 简单说一下：

• 同时意思是当二者都满足的时候才可以，有一个不满足就不行 ~
• 所以说，咱可以先判断能不能被3整除，如果都不能被3整除，直接输出不能即可，还谈什么同时整除，是吧
• 如果可以被3整除，接下来咱再判断能不能被5整除，如果5也可以整除，就说明可以同时整除，如果不能被5整除，就不是同时，就输出不能。

流程图

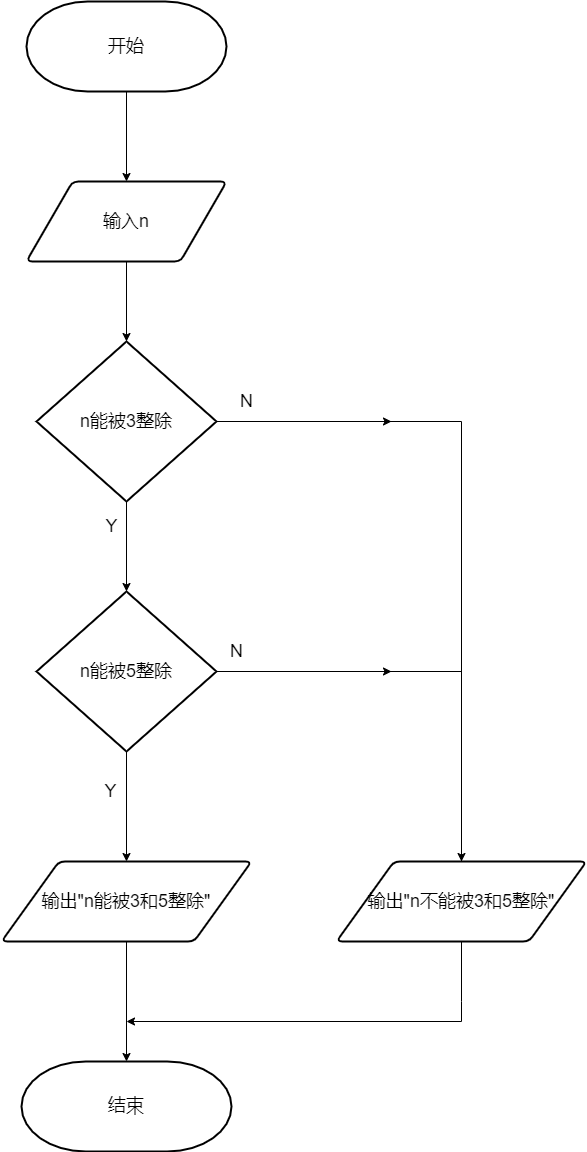
NS图

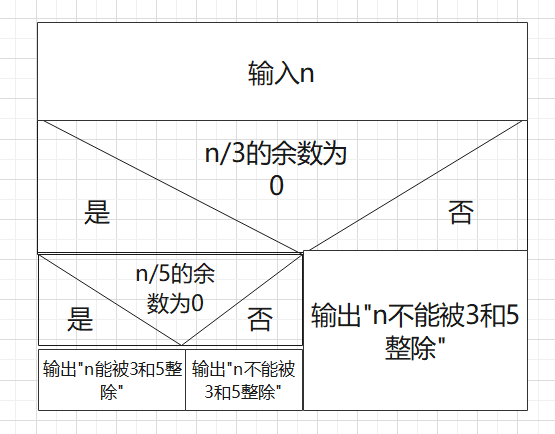
第六题

求两个数m和n的最大公约数。

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

问题分析

方法：辗转相除法，步骤如下。

• 2个数相除，大的除以小的得出余数
• 如果余数不为0，则拿较小的数与余数继续相除，判断新的余数是否为0
• 如果余数为0，则最大公约数就是本次相除中较小的数。

注意：0与另一个数的最大公约数是多少？

答：0除以任何一个数都得0 可以整除，所以0与一个数的最大公约数是这个数本身

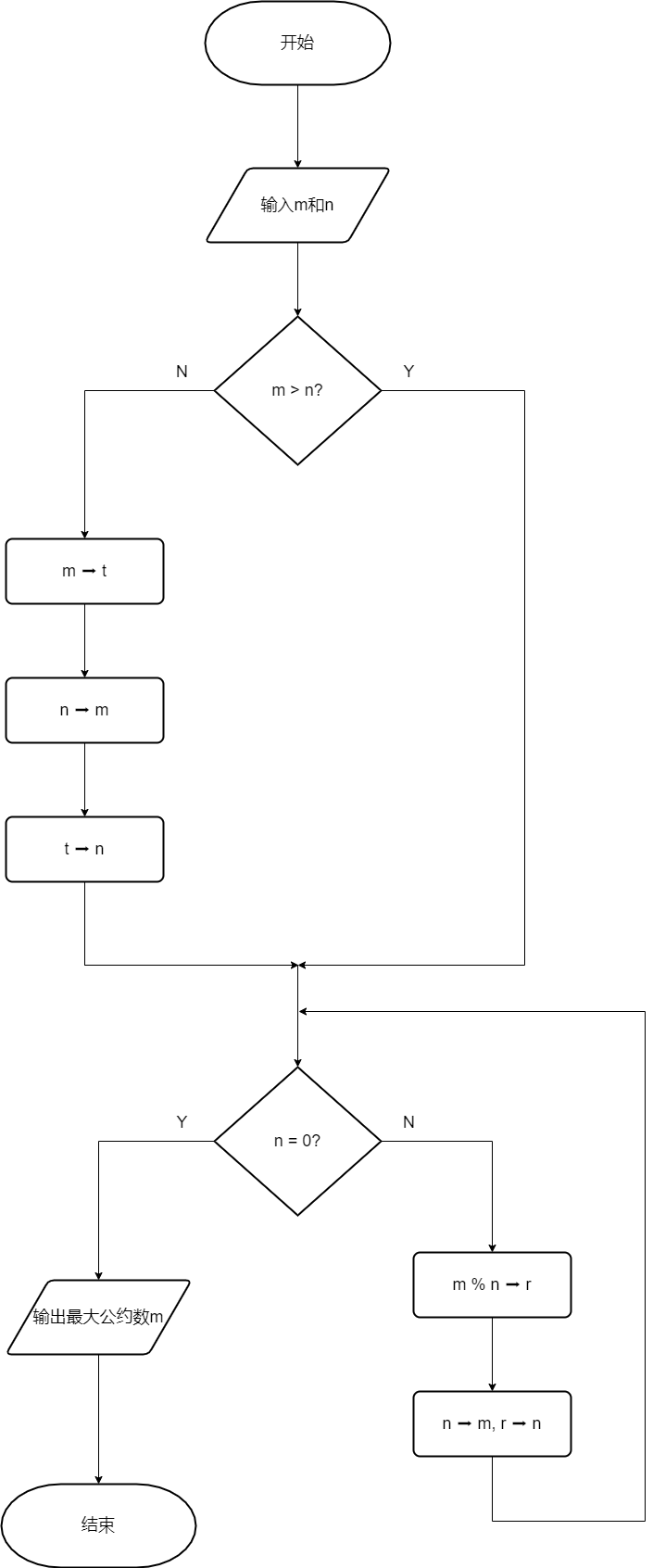
流程图和NS图解析：

• 输入两个数m和n，根据辗转相除法，先保证m大于n。
• 判断n是不是0，如果n是0的话，根据0的特点，直接可以得出m就是最大公约数。
• 如果n不是0，就让m除以n，获得余数r，把较小的数n传给m以便下一次求余数。
• 把余数r传给n，以便判断余数是不是0，并且方便下一次的求余。（因为r = m % n 是固定的，要想继续求余就得把要求余的两个数：较小的数和余数分别传给m和n）
• 如果余数为0，因为已经把余数传给n了，n是0的话就代表余数为0了。
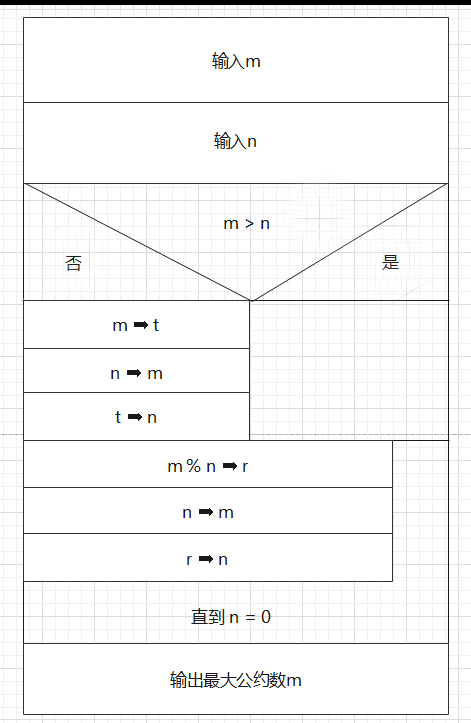
• NS图大同小异，就不解释了，试着理解

其实，这个辗转相除法不是那么好理解，如果一开始理解不了，可以试着先把这个算法记忆下来，慢慢理解。当然，也可以通过b站等教学网站，搜索相关视频或者参考百度来深入理解哦！实在理解不了也问题不大，并不是所有问题都需要理解的，会用就是了emmmmmmmm

流程图

NS图

第七题

求两个数m和n的最大公约数。

和第六题重复了，就跳过了

第八题

求一元二次方程式ax^2+bx+c=0的根，分别考虑有两个不相等的实根和有两个相等的实根两种情况。

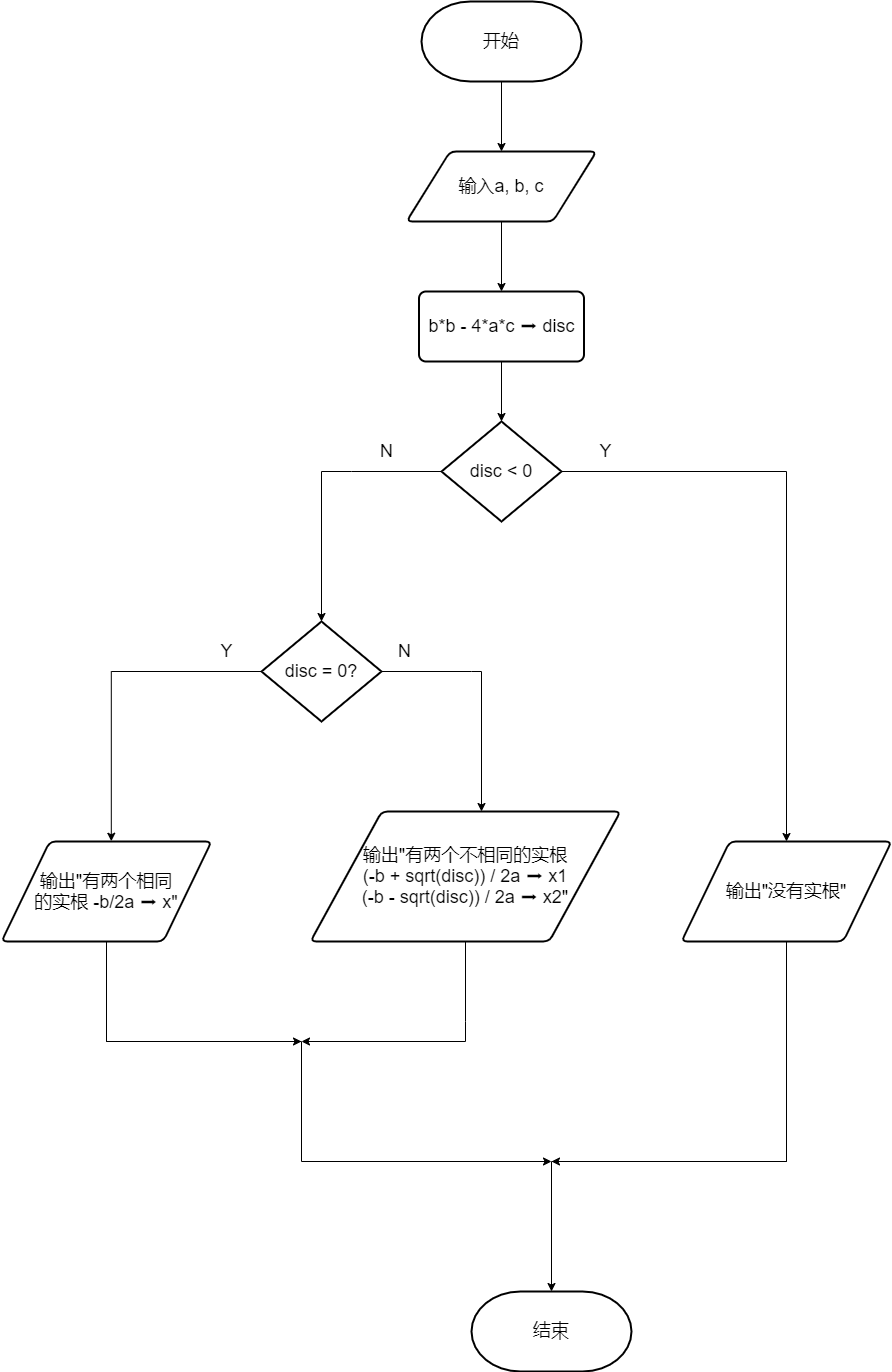
问题分析

相信能够看到这儿的，这道题对你来说已经非常简单了emmmmm，我感觉张老师出这道题的目的也是在于锻炼大家的基本素养，毕竟刚学，刷题刷的少，画的也少emmmmm 感觉没啥好解释的，简单分析一下吧：

• disc用来存放德尔塔的值
• sqrt是开根号的运算符
• 相信我不说大家也能猜出来，都是初中高中知识，真的觉得没什么好说的，就到这儿吧，已经深夜1.30了 室友正在酣睡中······ 不早了，晚安~

流程图

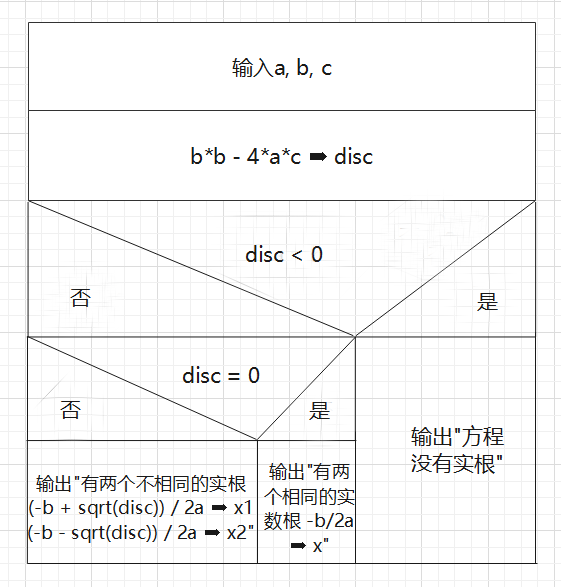
NS图